There is some holiday coming up. Can't quite think of what it is... I'll have to ask my wife. She knows these things. I hope it's not my anniversary, cuz she would get upset with me if I forgot that. I am pretty sure that our anniversary is in December or March or something, so I think I'm in the clear.
Anyway...
The half-wing function
Let's start with a polynomial equation, we'll call it p(x). I will define it as the sum of three polynomials:
The first of these polynomials, p1(x), is linear in x. I'll have it going from k1 at x = 0, down to 0 at x=pi .
The second polynomial, p2(x), will be 0 at both ends and a second degree parabola in between. In this way, no matter how big I scale it (by using my handy k2 parameter, it won't affect the value of p(x) at the ends. Whenever I get a chance to do this with a polynomial, I go for it.
I have one more polynomial, we'll make this one a cubic parabola. This one will get nailed down at the ends (x = 0 and x=pi), and will also be zero halfway in between.
I can pick values for the three parameters to give me any cubic polynomial that goes through (0, k1) and (pi, 0). How cool is that? Just for kicks, I chose k1 = 2.0, k2 = 0.3, and k3 = 0.6. The plot below shows the very agreeable cubic polynomial that is generated this way.
The half-wing function
I could have just played with the standard (canonical) form of the cubic parabola, but that gets confusing. with this formulation, k1 allows me to adjust the starting height, k2 allows me to adjust the amount of torsional wiggle, that is, how much the left half bows down and the right half bows the other way. Finally, the k3 parameter allows me to adjust the midpoint up and down.
I did a little work with this idea of expressing polynomials differently a while ago. One particularly cool thing is that this leads to a way to do regression that always goes through some fixed points.
The full-wing function
I like that function, but I would like to see the other half of the wing. I can use the absolute value function to flip this function over. Now the variable along the abscissa is z. I use z to get x, and then plug x into the equation for p. Back when I was teaching algebra, I would say that the absolute value function is like a tavern. Whether you are negative or positive going in, you will always be positive coming out.
The flipping function
This flipping over function gives me a wonderful plot of a pair of sea gull wings, symbolizing peace, since sea gulls are very peaceful animals and never hurt another living thing. Or maybe the plot looks like a champagne glass. That kinda reminds me of some holiday, but I can't quite place it.
The full-wing plot
Going polar
Sea gulls sometimes go to the North Pole. Or maybe that's penguins. I dunno. Some bird flies up to there. Anyway, that whole polar thing gets me thinking about (what else) polar coordinates. The full-wing plot already goes from 0 to 2pi. Maybe I should plot it in polar coordinates? Here is how I get from one to the other.
Now it's just a matter of plugging it all into Excel. I entered all this stuff into a spreadsheet. I let z go from 0 to 2pi in kinda small steps. I computed x by using the flipping function. I computed p(x), with the values of the k parameters. And these all went into computing a sequence of (x, y) values. Just for grins, I decided to plot them.
Now that I have the blog written, I need to go find out what day I was supposed to be remembering!
I christen this function the Madeloid, in honor of my wife, the Gypsy Songstress, the Shopping Maven, the love of my life.
Would you like a copy of the spreadsheet that created this? Send me an email at john@johnthemathguy.com.


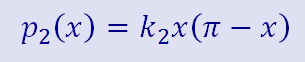


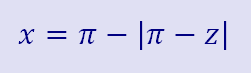



They say that "Love hurts"...well, my head hurts from all this math. LOL Nice blog, sir!
ReplyDeleteThank you Joel! Next up... the equation for Barry White.
ReplyDeleteA long time ago, before Postscript, we had to add quality text to a slide making system. Based on a "hack memo" we put together parametric bezier curve equations, with only a few control points on the final curve, initial and ending angles, and fixed velocities, which enabled us to quickly copy Letraset letters. We demo'd it by make almost that exact heart curve. One (L/R) side of the heart required setting only 4 points: 1 - the top center start point at near 90 degree (upward) starting direction, 2 - the top peak point with start/stop direction horizontal, 3 - the side point with start/stop directions vertical and 4 - the bottom end point with ending tangent direction adjusted. 30 seconds to make a perfect half heart - no user math! Once we had those 3 parametric bezier sections, recursive evaluation using successive midpoints of curves until error was less than 1 pixel enabled quick evaluation even on IBM XT!
ReplyDelete