My little buddy here is intent on an important task. He is trying to organize his crayons.
Go ahead, make my gray!
You may think this is an easy task, organizing crayons, but you would be wrong. At least, that is, if you are an adult. I distributed crayons to a group of first and second graders. I set them loose in a gym and asked them to organize themselves by color. It took maybe ten or fifteen minutes, but they did it. I gave the same task to a group of managers in a large corporation that shall go nameless. They held preliminary meetings with action items for subcommittees to perform market analysis, develop a business case, and research environmental impacts. Project leaders were appointed to develop realistic estimates of timelines, and to do risk analysis. I expect them to get back to me by mid-June with a detailed action plan. They got started back in September of 2007.
Arranging crayons in a line
One possible way to arrange crayons is by the colors of the rainbow. I pulled 13 crayons out of my favorite box of crayons and made a nice lineup which I call the "craynbow" [1]. You can see red, red-orange, orange-red, orange, yellow-orange, orange-yellow, yellow, and so on.
The craynbow
I know this is completely atypical of me, but I sort of told a lie. The last two crayons on the top, the red-violet and violet-red, are not actually in the rainbow. The most startling difference between the rainbow and the craynbow is that the rainbow is two crayons short of a full deck. This is probably obvious, but the additional two crayons form a bridge that allows us to connect the bottom of the craynbow to the top. Thus, the 13 crayons can be laid out in a circle.
But there are just a few other crayons that didn't make the cut. Most notably, the craynbow is missing white, gray, black, pink, and brown. Also the craynbow does not have a spot for lavender, burnt sienna, periwinkle, or maroon [2]. There are 96 crayons in my box, and 83 of them don't have a spot reserved for them in the craynbow. You don't have to be the sharpest crayon in the shed to see that you can't arrange a box of crayons in a single line in a way that chromatically feels good [3].
Color is three-dimensional
There is a simple reason why we can't put all the colors in a line. Color is three-dimensional. The craynbow looks at just one of those three dimensions of color, that is, the hue. Us color theory guys have two additional attributes that we assign to colors: chroma and lightness.
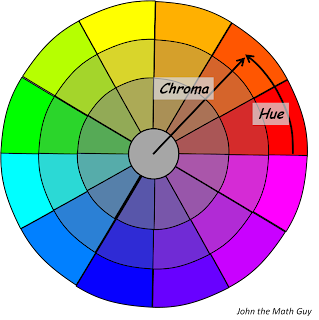
Showing hue and chroma
Let's start out with those 12 crayons arranged around in a circle. (I don't know what happened to the 13th crayon, by the way. Maybe it fell behind the couch.) What happens if we mix each of those crayons with a little gray, and then with a lot of gray? The results are shown in the really nifty circle below. Feel free to drop the artist an email telling him just how much you like the circle.
Color is three-dimensional
There is a simple reason why we can't put all the colors in a line. Color is three-dimensional. The craynbow looks at just one of those three dimensions of color, that is, the hue. Us color theory guys have two additional attributes that we assign to colors: chroma and lightness.
Showing hue and chroma
Let's start out with those 12 crayons arranged around in a circle. (I don't know what happened to the 13th crayon, by the way. Maybe it fell behind the couch.) What happens if we mix each of those crayons with a little gray, and then with a lot of gray? The results are shown in the really nifty circle below. Feel free to drop the artist an email telling him just how much you like the circle.
This cool drawing took me four hours to draw
Now for the cool part. Any color in this circle can be identified by naming the hue (the original crayon) and the chroma (how far it is from gray). The hue in this circle is the crayon that you started with. The chroma tells us how much gray was mixed in, that is, how rich the color is.
By the way, if you happen to be into analytic geometry, you might realize that hue and chroma are polar coordinates for the color plane. If, on the other hand, you don't really care all that much about anal retentive geometry, then you probably don't care about whether your polars coordinate.
Showing lightness and chroma
This next image demonstrates how lightness (along the up and down axis) combines with chroma (along the right to left axis). All the colors in this image have the same hue, yellow-red (5YR) [4].
A page from the "Munsell HVC Color Charts"
(It took me four hours to put these paint chips in order.)
(It took me four hours to put these paint chips in order.)
Along the left edge, we see a scale of colors that go from black up to white, all with just a tiny bit of orange flavoring to them. As we move to the right, there is more and more orange added--that is higher chroma.
Notice that we just don't get all that many shades of orange-black. As you add orange (or yellow) to black, it just has to get lighter. Thus, there is only one shade of orange on the bottom row. On the other hand, you can add orange to white without significantly decreasing its lightness. So, there are four shades of orange in the top row. The most saturated orange is basically still a pretty bright color. Blue and purple work pretty much the opposite way. Adding blue or purple to a pale gray will necessarily make it darker. It is possible to have a very saturated blue or purple that is also very dark.
Notice that we just don't get all that many shades of orange-black. As you add orange (or yellow) to black, it just has to get lighter. Thus, there is only one shade of orange on the bottom row. On the other hand, you can add orange to white without significantly decreasing its lightness. So, there are four shades of orange in the top row. The most saturated orange is basically still a pretty bright color. Blue and purple work pretty much the opposite way. Adding blue or purple to a pale gray will necessarily make it darker. It is possible to have a very saturated blue or purple that is also very dark.
These three attributes can be put together to create a color tree. The pages (like the one above called 5YR) are bound together at the left edge, and fanned out as shown in the very detailed and elaborate illustration below.
Here is another four hours of my life spent in Photoshop
Such a color tree was devised by Albert Munsell in the early 1900s. It is a testament to his genius and meticulousness that you can still buy a facsimile of this color tree almost a full century later. Not only that, but the guy actually has a blog, despite the fact that he died in 1918. He must be a ghost writer, I guess.
A very attractive model shows the Munsell color tree
Someday I will write a blog post about how this guy Munsell laid the foundation for the ever-popular color space CIELAB, and came to be known as the Father of Color Science. He was also the father of A. E. O. Munsell, who carried on his work. I don't intend to write a blog post about how Albert became the father of A. E. O.
What this all means
The first message is that you need three dimensions to organize a box of crayons. That's cool, but the more important message is that with the colors organized and quantified like this, it is possible to put a unique identifier on each color. All you need to do is specify the hue, chroma, and lightness, and you can unambiguously label any color. This might not be as romantic as using words like vermilion or aubergine, but it's a darn sight more precise. What young lady wouldn't prefer to hear poetry that scientifically specifies the color of her rosy cheeks?
----------------------------
[1] A major supercomputer company is developing a computer just to compute all the colors in the universe. The computer will be called the Cray-Ola.
[2] A ship loaded with red paint collided with a ship loaded with blue paint. All the crew were marooned.
[3] I used to tell my color classes just that you can't arrange your crayons all in a line in a way that made sense. Some smart alec said "Sure you can. Alphabetically!"
[4] I understand that some people might be so silly as to call the color "5YR" by the pedestrian name "orange". Please try not to laugh at them, ok? (My wife told me that I should point out that I'm being sarcastic here.)
[2] A ship loaded with red paint collided with a ship loaded with blue paint. All the crew were marooned.
[3] I used to tell my color classes just that you can't arrange your crayons all in a line in a way that made sense. Some smart alec said "Sure you can. Alphabetically!"
[4] I understand that some people might be so silly as to call the color "5YR" by the pedestrian name "orange". Please try not to laugh at them, ok? (My wife told me that I should point out that I'm being sarcastic here.)