Why is it called "regression"?

Regression. Such a strange name to be applied to our good friend, the method of least-squares curve fitting. How did that happen?

My dictionary says that regression is the act of falling back to an earlier state. In psychiatry, regression refers to a defense mechanism where you regress – fall back – to a younger age to avoid dealing with the problems that us adults have to deal with. Boy, can I relate to that!

All statisticians recognize the need for regression

Then there’s regression therapy, and regression testing…

Changing the subject radically, the “method of least squares” is used to find the line or curve that "best" goes through a set of points. You look at the deviations from a curve – each of the individual errors in fitting the curve to the points. Each of these deviations is squared and then they are all added up. The least squares part comes in because you adjust the curve so as to minimize this sum. When you find the parameters of the curve that give you the smallest sum, you have the least squares fit of the curve to your data.

For some silly reason, the method of least squares is also known as regression. It is perhaps an interesting story. I have been in negotiations with Random House on a picture book version of this for pre-schoolers, but I will give a preview here.

Prelude to regression

Let’s scroll back to the year 1766. Johann Titius has just published a book that gave a fairly simple formula that approximated the distances from the Sun to all the planets. Titius had discovered that if you subtract a constant from the size of the each orbit, the planets all fell in a geometric progression. After subtracting a constant, each planet was twice as far from the Sun as the one previous. Since Titius discovered this formula, it became known as Bode’s law.

I digress in this blog about regressing. Stigler’s law of eponymy says that all scientific discoveries are named after someone other than the original discoverer. Johann Titius stated his law in 1766. Johann Bode repeated the rule in 1772, and in a later edition, attributed it to Titius. Thus, it is commonly known as Bode’s law. Every once in a while it is called as the Titius-Bode law.

The law held true for six planets: Mercury, Venus, Earth, Mars, Jupiter, and Saturn. This was interesting, but didn’t raise many eyebrows. But when Uranus was discovered in 1781, and it fit the law, people were starting to think seriously about Bode’s law. It was more than a curiosity; it was starting to look like a fact.

But there was just one thing I left out about Bode’s law – the gap between Mars and Jupiter. Bode’s law worked fabulous if you pretended there was a mysterious planet between these two. Mars is planet four and we will pretend that Jupiter is planet six. Does planet five exist?

Now where did I put that fifth planet???

Scroll ahead to 1800. Twenty four of the world’s finest astronomers were recruited to go find the elusive fifth planet. On New Year’s Day of 1801, the first day of the new century, a fellow by the name of Giuseppe Piazzi discovered Ceres. Since it was moving with respect to the background of stars, he knew it was not a star, but rather something that resided in our the solar system. At first Piazzi thought it was a comet, but he also realized that it could be the much sought after fifth planet.

How could he decide? He needed to have enough observations over a long enough time period of time so that the orbital parameters of Ceres could be determined. Piazza observed Ceres a total of 24 times between January 1 and February 11. Then he fell ill, suspending his observations. Now, bear in mind that divining an orbit is a tricky business. This is a rather short period of time from which to determine the orbit.

It was not until September of 1801 that word got out about this potential planet. Unfortunately, Ceres had slipped behind the Sun by then, so other astronomers could not track it. The best guess at the time was that it should again be visible by the end of the year, but it was hard to predict just where the little bugger might show his face again.

Invention of least squares curve fitting

Enter Karl Friedrich Gauss. Many folks who work with statistics will recall his name in association with the Gaussian distribution (also known as the normal curve and the bell curve). People who are keen on linear algebra will no doubt recall the algorithm called “Gaussian elimination”, which is use to solve systems of linear equations. Physicists are not doubt aware of the unit of measurement of the strength of a magnetic field that was named after Gauss. Wikipedia currently lists 54 things that were named after Gauss.

More digressing...As is the case of every mathematical discovery, the Gaussian distributions was named after the wrong person.The curve was discovered by De Moivre. Did I mention Stigler? Oh... while I am at it, I should mention that Gaussian elimination was developed in China when young Gauss was only -1,600 years old.. Isaac Newton independently developed the idea about 1670. Gauss improved the notation in 1810, and thus the algorithm was named after him.

Back to the story. Gauss had developed the idea of least squares in 1795, but did not publish it at the time. He immediately saw that the Ceres problem was an application for this tool. He used least squares to fit a curve to the existing data in order to ascertain the parameters of the orbit. Then he used those parameters to predict where Ceres would be when it popped its head out from behind the Sun. Sure enough, on New Year’s eve of 1801, Ceres was found pretty darn close to where Gauss had said it would be. I remember hearing a lot of champagne corks popping at the Gaussian household that night! Truth be told, I don't recall much else!

From Gauss' 1809 paper "Theory of the Combination of Observations Least Subject to Error"

The story of Ceres had a happy ending, but the story of least squares got a bit icky. Gauss did not publish his method of least squares until 1809. This was four years after Adrien Marie Legendre’s introduction of this same method. When Legendre found out about Gauss’ claim of priority on Twitter, he unfriended him on FaceBook. It's sad to see legendary historical figures fight, but I don't really blame him.

In the next ten years, the incredibly useful technique of regression became a standard tool in many scientific studies - enough so that it became a topic in text books.

Regression

So, that’s where the method of least squares came from. But why do we call it regression?

I’m going to sound (for the moment) like I am changing the subject. I’m not really, so bear with me. It’s not like that one other blog post where I started talking about something completely irrelevant. My shrink says I need to work on staying focused. His socks usually don't match.

Let’s just say that there is a couple, call them Norm and Cheryl (not their real names). Let’s just say that Norm is a pretty tall guy, say, 6’ 5” (not his real height). Let’s say that Cheryl is also pretty tall, say, 6’ 2” (again, not her real height). How tall do we expect their kids to be?

I think most people would say that the kids are likely to be a bit taller than the parents, since both parents are tall – they get a double helping of whatever genes there are that make people tall, right?

One would think the kids would be taller, but statistics show this is generally not the case. Sir Francis Galton discovered this around 1877 and called it “regression to the mean”. Offspring of parents with extreme characteristics will tend to regress (move back) toward the average.

Why would this happen?

As with most all biometrics (biological measurements), there are two components that drive a person’s height – nature and nurture, genetics and environment. I apologize in advance to the mathaphobes who read this blog, but I am going to put this in equation form.

Actual Height = Genetic height + Some random stuff

Here comes the key point: If someone is above average in height, then it is likely that the contribution of “some random stuff” is a bit more than average. It doesn’t have to be, of course. Someone can still be really tall and still shorter than genetics would generally dictate. But, if someone is really tall, it’s likely that they got two scoops: genetics and random stuff.

So, what about the offspring of really tall people? If both parents are really tall, then you would expect the genetic height of the offspring to be about the same as that of the parents, or maybe a bit taller. But (here comes the second part of the key point) if both parents were dealt a good hand of random stuff, and the hand of random stuff that the children are dealt is average, then it is likely that the offspring will not get as good a hand as the parents. 

The end result is that the height of the children is a balance between the upward push of genetics and the downward push of random stuff. In the long run, the random stuff has a slight edge. We find that the children of particularly tall parents will regress to the mean.

We expect the little shaver to grow up to be a bit shorter than mom and pop

Galton and the idea of "regression towards mediocrity"
Francis Galton noticed this regression to the mean when he was investigating the heritability of traits, as first described in his 1877 paper Typical Laws of Heredity. He started doing all kinds of graphs and plots and stuff, and chasing his slide rule after bunches of stuff. He later published graphs like the one below, showing the distribution of the heights of adult offspring as a function of the mean height of their parents.

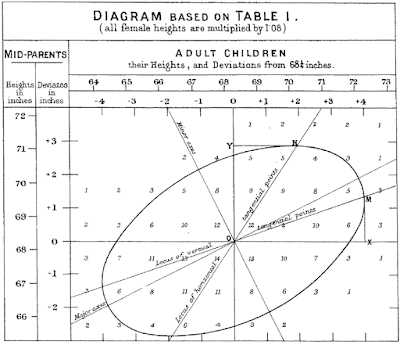
From Galton's paper "Regression towards mediocrity in hereditary stature", 1886

(For purposes of historical accuracy, Galton's 1877 paper used the word revert. The 1886 paper used the word regression.)

In case you're wondering, this is what we would call a two-dimensional histogram. Galton's chart above is a summary of 930 people and their parents. You may have to zoom in to see this, but there are a whole bunch of numbers arranged in seven rows and ten columns. The rows indicate the average height of the parent, and the columns are the height of the child. Galton laid these numbers out on a sheet of paper (like cells in a spreadsheet) and had the clever idea of drawing a curve that traced through cells with similar values. He called these curves isograms, but the name didn't stick. Today, they might be called contour lines; on a topographic plot, they are called isoclines, and on weather maps, we find isobars and isotherms.   

Galton noted that the isograms on his plot of heights were a set of concentric ellipses, one of which is shown in the plot above. The ellipses were all tilted upward on the right side.

As an aside, Galton's isograms were the first instance of ellipsification that I have seen. Coincidentally, the last blog post that I wrote was on the use of ellipsification for SPC of color data. I was not aware of Galton's ellipsification when I started writing this blog post. Another example of the fundamental inter-connectedness of  all things. Or an example of people finding patterns in everything!

Galton did not give a name to the major axis of the ellipse. He did speak about the "mean regression in stature of a population", which is the tilt of the major axis of the ellipse. From this analysis, he determined that number to be 2/3, which is to say, if the parents are three inches taller than average, then we can expect (on average) that the children be two inches above average.

So, Galton introduced the word regression into the field of statistics of two variables. He never used it to describe a technique for fitting a line to a set of data points. In fact, the math he used to derive his mean regression in stature bears no similarity to the linear regression by least squares that is taught in stats class. Apparently, he was unaware of the method of least squares.

Enter George Udny Yule
George Udny Yule was the first person to misappropriate the word regression to mean something not related to "returning to an earlier state". In 1897, he published a paper called On the Theory of Correlation in the Journal of the Royal Statistical Society. In this paper, he borrowed the concepts implied by the drawings from Galton's 1886 paper, and seized upon the word regression. In his own words (p. 177), "[data points] range themselves more or less closely round a smooth curve, which we shall name the curve of regression of x on y." In a footnote, he mentions the paper by Galton and the meaning that Galton had originally assigned to the word.

In the rest of the paper, Yule lays out the equations for performing a least squares fit. He does not claim authorship of this idea. He references a textbook entitled Method of Least Squares (Mansfield Merriman, 1894). Merriman's book was very influential in the hard sciences, having been first published in 1877, with the eighth version in 1910.

So Yule is the guy who is responsible for bringing Gauss' method of least squares into the social sciences, and in calling it by the wrong name.

Yule reiterates his word choice in the book Introduction to the Theory of Statistics, first published in 1910, with the 14th edition published in 1965. He says: In general, however, the idea of "stepping back" or "regression" towards a more or less stationary mean is quite inapplicable ... the term "coefficient of regression" should be regarded simply as a convenient name for the coefficients b1 and b2.

So. There's the answer. Yule is the guy who gave the word regression a completely different meaning. How did his word, regression, become so commonplace, when "least squares" was a perfectly apt word that had already established itself in the hard sciences? I can't know for sure.

The word regression is a popular word on my bookshelf

Addendum

Galton is to be appreciated for his development of the concept of correlation, but before we applaud him for his virtue, we need to understand why he spent much of his life measuring various attributes of people, and inventing the science of statistics to make sense of those measurements.

Galton was a second cousin of Charles Darwin, and was taken with the idea of evolution. Regression wasn't the only word he invented. He also coined the word eugenics, and defines it thus:

"We greatly want a brief word to express the science of improving stock, which is by no means confined to questions of judicious mating, but which, especially in the case of man, takes cognisance of all influences that tend in however remote a degree to give to the more suitable races or strains of blood a better chance of prevailing speedily over the less suitable than they otherwise would have had. The word eugenics would sufficiently express the idea..."

Francis Galton, Inquiries into Human Faculty and its Development, 1883, page 17

The book can be summarized as a passionate plea for the need of more research to identify and quantify those traits in humans that are good versus those which are bad. But what should be done about traits that are deemed bad? Here is what he says:

"There exists a sentiment, for the most part quite unreasonable, against the gradual extinction of an inferior race. It rests on some confusion between the race and the individual, as if the destruction of a race was equivalent to the destruction of a large number of men. It is nothing of the kind when the process of extinction works silently and slowly through the earlier marriage of members of the superior race, through their greater vitality under equal stress, through their better chances of getting a livelihood, or through their prepotency in mixed marriages."

Ibid, pps 200 - 201

It seems that Galton favors a kindler, gentler form of ethnic cleansing. I sincerely hope that all my readers are as disgusted by these words as I am.


This blog post was edited on Dec 28, 2017 to provide links to the works by Galton and Yule.

Blue skaters

A friend of mine, Renzo Shamey, was recently quoted by the New York Times. Well, I would like to think he's a friend of mine. More accurately, I would like you to think he's a friend of mine. I mean, he was quoted in the New York Times! What does that tell you about how great I am?!?!?

The article was about speedskaters, and how there is now a propensity for speedskaters to wear blue uniforms. It makes then faster.

The guy in blue is sooooo much faster than the other guy!

Havard Myklebus, a Norwegian sports scientist, explains the science behind the color choice. Quoting from the NYT article:

“What I’ve said is, our new blue suit is faster than our old red suit,” he [Havard] said with a tight smile, “and I stand by that.”

Here is another quote from the article along the same lines:

“It’s been proven that blue is faster than other colors,” said Dai Dai Ntab, a sprint specialist for the Netherlands.

So. There you have it. Blue is faster. This is born out in the animal kingdom. Umm... maybe not.

Fastest animals on land, in sea, in sky, and on sliderule

My best friend, Renzo, explains the science this way:

... based on my knowledge of dye chemistry, I cannot possibly imagine how dyeing the same fabric with two dyes that have the same properties to different hues would generate differing aerodynamic responses.

A brief, but well-deserved rant

The two answers illustrate the dichotomy of Science. Note the capital S. This indicates that the word should be said in an intense whisper -- with great reverence. On the one hand, Science is a book about everything that we know. We look to Science to explain how and why something works. This is the Science that my long-time buddy Renzo was referring to.

A cherished book from my childhood

Havard, who I'm sure would be a bosom-buddy of mine if I ever met him, is hearkening to the other half of the dichotomy of Science, the half that is more of a verb then a noun. This view of Science is more along the lines of "I poured the stuff in the beaker-thingie. When I stirred it, it blew up and singed off one of my eyebrows. I dunno why, but when I repeated the experiment, my other eyebrow was gone."

Science is both the floor wax that underlays our method of the pursuit of knowledge, and the dessert topping of sweet knowledge that we get from this holy pursuit.

(I sincerely hope that sentence makes it into the Guinness Book of World Records for the most beautiful allusion to an SNL skit to help explain the nature of Science. My Dad would have been proud.)

I mention this Science thing cuz I got a bee in my bonnet. When a person who is into homeopathy, or anti-vaxxing, or astrology is presented with Science, they often respond with "Oh, yeah? Well, Science doesn't know everything!" Perhaps Science-As-A-Noun doesn't have a cure for cancer, can't explain why some sub-atomic particles are cuter than others, and can't tell me why I didn't exercise yesterday, but Science-As-A-Verb provides us with a method that will ultimately answer the first two of those questions. And Science-As-A-Verb has demonstrated that homeopathy is ineffective, vaccines are good, and astrology is bogus.

Enough of my rant. Let's get back to the speed of blue.

Faster than a speeding differential equation because of the blue suit?

Psychochromokinesiology

Here is a quote of Renzo's that did not make it into the NYT article:

Psychologically we are influenced by the colors we wear, in fact I am running a study on this very topic at the moment in North Carolina State and our reactions can be influenced by this also.  It has been shown that reaction responses when people are shown red tends to be faster.

Did I mention that Renzo is my closest (and just about only) friend? I look forward to hearing more about his experiment. I have always been fascinated about the intersection between psychology and color science. Full disclaimer; I am a color scientist, but I am not a psychologist. But, I do have psychology. Just ask my therapist. Or my wife.

Color no doubt effects feelings, and it is only logical that this should apply to sports. After all, Dr. Yogi Berra once said: "Baseball is 90 per cent mental. The other half is physical."

Black and aggression

Can you guess which guy is the bad guy?

The earliest study on Psychochromokinesiology that I found was from 1988, The Dark Side of Self- and Social Perception: Black Uniforms and Aggression in Professional Sports. They found that the man in black is more likely to go to the penalty box than athletes wearing other colors.

An analysis of the penalty records of the National Football League and the National Hockey League indicate that teams with black uniforms in both sports ranked near the top of their leagues in penalties throughout the period of study.

But, cause or effect? Did they receive more penalties because wearing black makes an athlete more aggressive? Or is this a case of the don't-drive-a-red-car-cuz-the-cops-are-more-likely-to-pull-you-over syndrome? The researchers set up experiments to test both explanations. It turned out that both were true.

Red and performance

Danger, Gene!

But wearing red might be a good thing, perhaps because of the effect on the other team. Red means danger, right? Here is a quote from one study, Psychology: Red enhances human performance in contests, published in Nature:

...across a range of sports, we find that wearing red is consistently associated with a higher probability of winning.

Here is another really technical sounding paper, Red shirt colour is associated with long-term team success in English football, that gives a shout out to red:


A matched-pairs analysis of red and non-red wearing teams in eight English cities shows significantly better performance of red teams over a 55-year period.

Two out of two technical papers choose red uniforms. But why would it matter?

Color's effect on the perception of others

The kids with the red uniforms always got picked first for dodge ball

Another study tried to figger out what went on in the mind of a goalie: Soccer penalty takers' uniform colour and pre-penalty kick gaze affect the impressions formed of them by opposing goalkeepers. They showed goalies video clips of soccer players taking penalty shots, and then asked the goalies for their opinions. The conclusion was that a penalty kicker was perceived as being more competent if they were wearing red than if they were wearing white.

Here is study that suggests that dominance of athletes in red uniforms might be due to bias in judging: When the Referee Sees Red.... In this study, the researchers created two versions of the 11 video clips from a tae kwon do match. The two versions were identical except that the color of the protective gear was switched. In one video, it was red versus blue, and in the other, it was blue versus red. You can watch one of the clips here. They sat 42 experienced referees down in front of the videos and asked them to count points for each athlete. Their results?

...competitors dressed in red are awarded more points than competitors dressed in blue, even when their performance is identical.

Summary

Black is meaner than other colors, and red wins more often than blue. Why is this? There is some evidence that a player changes his or her behavior because of the color they wear. There also is evidence that players react differently because of the colors that other players wear. And, there is also evidence that referees judge players differently based on the color of the uniform.

But I did not find any studies on why a blue uniform would make a skater faster. In the spirit of all research papers written by researchers looking for continued funding, let me say that more research is clearly necessary.

Statistics of multi-dimensional data, example

In the previous blog post, Statistics of multi-dimensional data, theory, I introduced a generalization of the standard deviation to three-dimensional data. I called it ellipsification. In this blog post I am going to apply this ellipsification thing to real data to demonstrate the application to statistical process control of color.

I posted this cuz there just aren't enough trolls on the internet

Is the data normal?

In traditional SPC, the assumption is almost always made that the underlying variation is normally distributed. (This assumption is rarely challenged, so we blithely use the hammers that are conveniently in our toolbox -- standard SPC tools -- to drive in screws. But that's another rant.)

The question of normalcy is worth addressing. First off, since I am at least pretending to be a math guy, I should at least pay lip service to stuff that has to do with math. Second, we are venturing into uncharted territory, so it pays to be cautious. Third, we already have a warning that deltaE color difference is not normal. Ok, maybe a bunch of warnings. Mostly from me.

I demonstrate in the next section that my selected data set can be transformed into another data set with components that are uncorrelated, have zero mean and standard deviation of 1.0, and which give every indication of being normal. So, one could us this transform on the color data and apply traditional SPC techniques on the individual components, but you will see that I take this one step further.

    Original data

I use the solid magenta data from the data set that I describe below in the section below called "Provenance of the data". I picked magenta because it is well known that it has a "hook". In other words, as you increase pigment level or ink film thickness, it changes hue. The thicker the magenta ink, the redder it goes. Note that this can be seen in the far left graph as a tilt to the ellipsoid.

I show three views of the data below. The black ellipses are slices through the middle of the ellipsification in the a*b* plane, the L*a* plane, and the L*b* plane, respectively.

View from above

View from the b* axis

View from the a* axis

    Standardized data

Recall for the moment when you were in Stats 201. I know that probably brings up memories of that cute guy or girl that sat in the third row, but that's not what I am talking about. I am talking about standardizing the data to create a Z score. You subtracted the mean and then divided by the standard deviation so that the standardized data set has zero mean, and standard deviation of 1.0.

I will do the same standardization, but generalized to multiple dimensions. One change, though. I need an extra step to rotate the axes of the ellipsoid so that all the axes are aligned with the coordinate axes. The cool thing is that the new scores (call them Z1, Z2, and Z3, if you like) are now all uncorrelated.

Geometrically, the operations are as follows: subtract the mean, rotate the ellipsoid, and then squish or expand the individual axes to make the standard deviations all equal to 1.0. The plot below show three views of the data after standardization. (Don't ask me which axes are L*, a*, and b*, by the way. These are not L*, a*, or b*.)

Standardized version of the L*, a*, and b* variation charts

Not much to look at -- some circular blobs with perhaps a tighter pattern nearer the origin. That's what I would hope to see. 

Here are the stats on this data:

	Mean	Stdev	Skew	Kurtosis
Z1	0.000	1.000	-0.282	-0.064
Z2	0.000	1.000	0.291	0.163
Z3	0.000	1.000	-0.092	-0.658

The mean and standard deviation are exactly 0.000 and 1.000. This is reassuring, but not a surprise. It just means that I did the arithmetic correctly. I designed the technique to do this! Another thing that happened by design is that the correlations between Z1 and Z2, and between Z1 and Z3 are both exactly 0.000. Again, not a surprise. Driving those correlations to zero was the whole point of rotating the ellipsoid, which I don't mind saying was no easy feat.

The skew and kurtosis are more interesting. For an ideal normal distribution, these two values will be zero. Are they close enough to zero? None of these numbers are big enough to raise a red flag. (In the section below entitled "Range for skew and kurtosis", I give some numbers to go by to scale our expectation of skew and kurtosis.)

In the typical doublespeak of a statistician, I can say that there is no evidence that the standardized  color variation is not normal. Of course, that's not to say that the standardized color variation actually is normal, but a statement like that would be asking too much from a statistician. Suffice it to say that it walks like normally distributed data and quacks like normally distributed data.

Dr. Bunsen Honeydew lectures on proper statistical grammar

This is an important finding. At least for this one data set, we know that the standardized scores Z1, Z2, and Z3 can be treated independently as normally distributed variables. Or, as we shall see in the next section, we can combine them into one number that has a known distribution.

Can we expect that all color variation data behaves this nicely when it is standardized by ellipsification? Certainly not. If the data is slowly drifting, the standardization might yield something more like a uniform distribution. If the color is bouncing back and forth between two different colors, then we expect the standardized distributions to be bi-modal. But I intend to look at a lot of color to try to see if 3D normal distribution is the norm for processes that are in control.

In the words of every great research paper every written, "clearly more research is called for".

The Zc statistic

I propose a statistic for SPC of color, which I call Zc. This is a generalization of the Z statistic that we all know and love. This new statistic could be applied to any multi-dimensional data that we like, but I am reserving the name to apply to three-dimensional data, in particular, to color data. (The c stands for "color". If you have trouble remembering that, then note that c is the first letter of my middle name.)

Zc is determined by first ellispifying the data set. The data set is then standardized, and then each data point is reduced to a single number (a scalar), as described in the plot below. The red points are a standardization of the data set we have been working with.the data set we have been working with. I have added circles at Zc of 1, 2, 3, 4. Any data points on one of these circles will have a Zc score of the corresponding circle. Points in between will have intermediate values, which are the distance from the origin. Algebraically, Zc is the sum in quadrature of the individual three components, that is to say, the square root of the sum of the squares of the three individual components.

A two-dimensional view of the Z scores

Now that we have standardized our data into three uncorrelated random variables that are (presumably) Gaussian with zero mean and unit standard deviation, we can build on some established statistics. The sum of the squares of our standardized variable will follow a chi-squared distribution, and the square root of the sums of the squares will follow a chi distribution. Note that this quantity is the distance from the data point to the origin.

Chi is the Greek version of our letter X. It is pronounced with the hard K sound, although I have heard neophytes embarrass themselves by pronouncing it with the ch sound. To make things even more confusing, there is a Hebrew letter chai which is pronounced kinda like hi, only with that rasping thing in the back of your throat. Even more confusing is the fact that the Hebrew chai looks a lot like the Greek letter pi, which is the mathematical symbol for all things circular like pie and cups for chai tea. But the Greek letter chi has nothing to do with either chai tea, or its Spoonerism tai chi.

Whew. Glad I got that outa the way.

Why is it important that we can put a name on the distribution? This gives us a yardstick from which to gauge the probability that any given data point belongs to the set of typical data. The table below gives some probabilities for the Zc distribution. Here is an example that will explain the table a bit. The fifth row of the table says that 97% of the data points that represent typical behavior will have Zc scores of less than 3.0. Thus the chance that a given data point will have a Zc score larger than that is 1 in 34.

Levels of significance of Zc

Zc	P(Zc)	Chance
1.0	0.19875	1
1.5	0.47783	2
2.0	0.73854	4
2.5	0.89994	10
3.0	0.97071	34
3.5	0.99343	152
4.0	0.99887	882
4.5	0.99985	6623
5.0	0.99999	66667

The graph below is a run time chart of the Zc scores for the 204 data points that we have been dealing with. The largest score is about 3.5. We would be hard pressed at calling this an aberrant point, since the table above says that there is a 1 in 152 chance of such data happening at random. By the way, we had close to 152 data points, so we should expect 1 data point above 3.5. A further test: I count eight data points where the Zc score is above 3.0. Based on the table, I expect about 6.

My conclusion is that there is nothing funky about this data.

Runtime chart for Zc of the solid magenta patches

Where do we draw the line between common cause and special cause variation? In traditional SPC, we use Z > 3 as the test for individual points. Note that for a normal distribution, the probability of Z < 3 is 0.99865, or one chance in 741 of Z < 3.0. This is pretty close to the probability of Zc < 4 for a chi distribution. In other words, if you are using Z > 3 as a threshold for QC with normally distributed data, then you should use Zc > 4 when using my proposed Zc statistic for color data. Four is the new three.

Provenance for this data

In 2006, the SNAP committee (Specifications for Newspaper Advertising Production) took on a large project to come to some consensus about what color you get when you mix specific quantities of CMYK ink on newsprint. A total of 102 newspapers printed a test form on its presses. The test form had 928 color patches. All of the test forms were measured by one very busy spectrophotometer. The data was averaged by patch type, and it became known as CGATS TR 002.

Some of the patches were duplicated on the sheet for quality control. In particular all of the solids were duplicated. Thus, in the blog post, I was dealing with 204 measurements of a magenta solid patch from 102 different newspaper printing presses.

Range for skew and kurtosis

How do we decide when a value of skew or kurtosis is indicative of a non-normal distribution? Skew should be 0.0 for normal variation, but can it be 0.01 and still be normal? Or 0.1? Where is the cutoff?

Consider this: the values for skew and kurtosis that we compute from a data set are just estimates of some metaphysical skew and kurtosis. If we asked all the same printers to submit another data set the following day, we would likely have a somewhat different value of all the statistics. If we had the leisure of collecting a Gillian or a Brilliant or even a vermillion measurements, we would have a more accurate estimate of these statistical measures. 

Luckily some math guy figgered out a simple formula that allows us to put a reliability on the estimates of skew and kurtosis that we compute.

Our estimate of skew has a standard deviation of sqrt (6 / N). For N = 204 (as in our case) this works out to 0.171. So, an estimate of skew that is outside of the range from -0.342 to 0.342 is suspect, and outside the range of -0.513 to 0.513 is very suspect.

For kurtosis, the standard deviation of the estimate is sqrt (24/N), which gives us a range of +/- 0.686 for suspicious and +/- 1.029 for very suspicious.

Statistics of multi-dimensional data, theory

This blog post is the culmination of a long series of blog posts on the statistics of color difference data. Most of them just basically said "yeah, normal stats don't work". Lotta help that is, eh? Several blog posts alluded to the fact that I did indeed have a solution. The most recent of which alluded to a method that works in the very title of the blog post: Statistical process control of color, approaching a method that works.

Now it's time to unveil the method.

Generalization of the standard deviation

One way of describing the technique is to call it a generalization of the standard deviation to multiple dimensions -- three dimensions if we are dealing with color data. That's a rather abstract concept, so I will explain.

     One dimensional standard deviation

We can think of our good friends, the standard deviation and mean, as describing a line segment on the number line, as illustrated below. If the data is normally distributed (also called Gaussian, or bell curve), then you would expect that about 68% of the data will fall on the line segment within one standard deviation unit (one sigma) of the mean, 95.45% of the data will fall within two sigma of the mean, and 99.73% of the data will be within three sigma of the mean.

As an aside, note that not all data is normally distributed. This holds true for color difference data, which is the issue that got me started down this path!

So, a one-dimensional standard deviation can be thought of as a line segment that is 2 sigma long, and centered on the mean of the data. It is a one-dimensional summary of all the underlying data.

     Two-dimensional standard deviation

Naturally, a two-dimensional standard deviation is a two-dimensional summary of the underlying two-dimensional data. But instead of a (one-dimensional) line segment, we get an ellipse in two dimensions.

In the simplest case, the two-dimensional standard deviation is a circle (shown in orange below) which is centered on the average of the data points. The circle has a radius of one sigma. If you want to get all mathematical about this, the circle represents a portion of a two-dimensional Gaussian distribution with 39% of the data falling inside the circle, and 61% falling outside.

Two dimensional histogram of a simple set of two dimensional data
The orange line encompasses 39% of the volume.

I slipped a number into that last paragraph that deserves to be underlined: 39%. Back when we were dealing with one-dimensional data, +/- one sigma would encompass 68% of normally distributed data. The number for two-dimensional data is 39%. Toto, I have a feeling we're not in one-dimensional-normal-distribution-ville anymore.

Of course, not all two-dimensional standard deviations are circular like the one in the drawing above. More generally, they will be ellipses. The the length of the semi-major and semi-minor axes of the ellipse are the major and minor standard deviation.

--- Taking a break for a moment

I better stop to review some pesky vocabulary terms. A circle has a radius, which is the distance from the center of the circle to any point on the circle. A circle also has a diameter, which is the distance between opposite points on the circle. The diameter is twice the radius.

When we talk about ellipses, we generally refer to the two axes of the ellipse. The major axis is the longest line segment that goes through the center of the ellipse. The minor axis is the shortest line segment that goes through the center of the ellipse. The lengths of the major and minor axes are essentially the extremes of the diameters of the ellipse. They run perpendicular to each other.

An ellipse, showing off the most gorgeous set of axes I've ever seen

There is no convenient word for the two "radii" of an ellipse. All we have is the inconvenient phrases semi-major axis and semi-major axis. These are half the length of the major and minor axes, respectively.

--- Break over, time to get back to work

The axes of the ellipses won't necessarily be straight up and down and left-to-right on a graph. So, the full description of the two-dimensional standard deviation must include information to identify the orientation of these axes.

The image below shows a set of hypothetical two-dimensional data that has been ellipsified. The red dots are random data that was generated using Mathematica. I asked it to give me 200 normally distributed x data points with a standard deviation of 3, and 200 normally distributed y data points  with a standard deviation of 1. These original data points (the x and y values) were uncorrelated.

This collection of data points were then rotated by 15 degrees so that the new x values had a bit of y in them, and the new y values had a bit of x in them. In other words, there was some correlation (r = 0.6) between the new x and y. I then added 6 to the new x values and 3 to the new y values to move the center of the ellipse. So, the red data points are designed to represent some arbitrary data set that could just happen in real life.

I performed an ellipsification, and have plotted the one, two, and three sigma ellipses (in pink). The major and minor axes of the one sigma ellipse are shown in blue.

Gosh darn! that's purdy!

The result of ellipsifying this data is all the parameters pertaining to the innermost of the ellipses in the image above. This is an ellipse that is centered on {6.11, 3.08}, with major axis of 3.19 and minor axis of 1.00. The ellipse is oriented at 15.8 degrees. These are all rather close to the original parameters that I started with, so I musta done sumthin right.

I also counted the number of data points within the three ellipses. I counted 38.5% in the 1 sigma ellipse, 88.5% in the 2 sigma ellipse, and 99% in the 3 sigma ellipse. (Of course when I say I did this, I really mean that Mathematica gave me a little help.) If the data follows a two-dimensional normal distribution, then the ellipses will encompass 39%, 86.5%, and 98.9% of the data. This is one indication that this condition is met.

The following pieces of information are determined in the ellipsification process of two-dimensional data:

     a) The average of the data which is the center of the ellipse (two numbers, for the horizontal and vertical values)
     b) The orientation of the ellipse (which could be a single number, such as the rotation angle)
     c) The lengths of the semi-major and semi-minor axes of the ellipse (two numbers)

The ellipsification can be described in other ways, but these five numbers will tell me everything about the ellipse. The ellipse is the statistical proxy for the whole data set.

     Three-dimensional standard deviation

The extension to three-dimensional standard deviation is "obvious". (Obvious is a mathematician's way of saying "I don't have the patience to explain this to mere mortals.")

The result of ellipsifying three-dimensional data is the following nine pieces of information that are necessary to describe an arbitrary (three-dimensional) ellipsoid:

    a) The average of the data (three numbers, for the average of the x, y, and z values)
    b) The orientation of the ellipsoid (three numbers defining the direction that the axes point)
    c) The lengths of the semi-major, semi-medial, and semi-minor axes of the ellipse (three numbers)

The image below is an ellipsification of real color data. The data is the color of a solid patch as produced by 102 different newspaper printing presses. There were two samples of this patch from each press, so the number of dots is 204.

The 204 dots were used to compute the three-dimensional standard deviation, which is represented by the three lines. The longest line, the red line, is the major axis of the ellipse, and has a length of 5.6 CIELAB units. The green and blue lines are the medial and minor axes, respectively. They 2.2 and 2.1 CIELAB units long. All three of the axes meet at the mean of all the data points, and all three are two-sigma long (+/-1 sigma from the mean). Depending on the angle you are looking, it may not appear that the axes are all perpendicular to each other, but they are.

Ellipsification of some real data, as shown with the axes of the ellipsoid

Trouble viewing the image above? The image is a .gif image, so you should see it rotating. If it doesn't, then try a different browser, or download it to your computer and view it directly.

What can we do with the ellipsification?

The ellipsification of color data is a three-dimensional version of the standard deviation, so in theory, we can use it for anything that we would use the standard deviation for. The most common use (in the realm of statistical process control) is to decide whether a given data point is an example of typical process variation, or if there is some nefarious agent at work. (Deming would call that a special cause.)

We will see an example of this on real data in the next blog post on the topic: Statistics of multi-dimensional data, example.

Can a light be gray?

I follow Quora. I am not saying I am proud of that, but at least I will admit it. I look for questions in my topic of expertise, which is to say, color. And of course, my motives for answering the questions are purely altruistic. Answering the questions is part of my crusade to overcome the general public's ignorance of that noblest of the Sciences, Color Science.

Or maybe I just like to hear myself talk.

Regardless of the reasons, here is a question that I recently answered. My answer has been embellished a bit for this blog post -- mostly to make me sound more important. But I also added some cool pictures.

Is there gray light?

This is an interesting question! I have some experiments that will answer the question.

First experiment

If you connect a white LED to a variable power supply, and gradually turn the voltage down, it will always appear white, even though gray is somewhere between full white and black. I show that in the image below. This is a white LED (color temperature of maybe 6500K) run at 2.4V. This is about as low as it will go without flickering out. The camera clearly sees it as white.

There is no way to suppress the whiteness of this LED

Don't have a variable power supply? You can buy a white LED flashlight and leave it on until the batteries almost run down to nuthin. The LEDs will still be white.

So, first answer: No, there ain't no such thing as gray light. 

Second experiment

But if your arrange those white LEDs into a matrix and call that matrix a computer screen, then you can dim a portion of those white LEDs and get gray. Yes, Virginia, there is gray light, and it's what's coming at you when you look at the image below! Contrary to the guy who wrote about the first experiment, you can make gray light with white LEDs.

You're looking at gray light, right this very minute!!

(I should clarify... some, but not all, computer displays use white LEDs as a backlight behind filters. The idea here is that in principle, you could make a computer display with white LEDs, and you could display gray on that screen.)

Third experiment

Turn your entire computer screen into “gray” (RGB values of 128, for example), and turn out the lights in your room. After a few minutes, you will perceive the screen as white.

I am totally dumbfounded by how white my gray screen looks
Or maybe just dumb? 

Why did that happen? Gray is not a perceivable color all by itself. To see it, you need a white to reference it to.

In the first experiment, the white LED is not putting out a huge amount of light, but the light from the white LED is all coming from a small point. This means that the intensity at that point is very, very high, and likely much brighter than anything else in your field of view.

In the second experiment, I didn’t say this, but it is likely that there are some pixels on your computer screen that are close to white (RGB=255), so the area with RGB=128 will appear gray in comparison. In the third experiment, the only white reference that you have is the computer screen itself, so once your eyes have accommodated to the new lighting, the computer screen will be perceived as white.

Fourth experiment

I came up with a startling way to demonstrate this idea that "gray is perceived only in comparison to a reference white". Brilliant idea, really. I used the same set up I did for that first cool picture of a white LED. But in this case, I used two LEDs, wired in series. Note that I had to crank up the voltage to 4.8V. Electricity passes through each of the LEDs, so in principle they produce the same amount of total light.

The difference between the two LEDs is that the one on the right doesn't have a clear plastic bubble -- the plastic bubble on the LED on the right is a translucent white. The one on the right is a diffuse LED. The light from the diffuse LED is about the same, but it is spread out over a larger area, and not focused, so the amount of light hitting my eye is much less.

My camera saw the diffuse LED as being somewhat dimmer than the one on the left. Maybe from the picture you would call this a gray LED? My eyes looked at the two white LEDs and saw the one on the right as being gray. Honest to God, it was emitting gray light. My eyes saw the LED on the left, and used that as the white reference. The fact that I was drinking heavily during this fourth experiment is largely irrelevant.

Today's special - gray LEDs

So, I can definitively say that "gray" light exists, since I built a system with both a white and a gray LED. I'm sure if I would have introduced this a few weeks ago, I would have gotten an early morning call from Mr. Nobel about some sort of prize. Well, maybe next year. I will try to look surprised.

Moral

This blog has to have a moral. It was a bit hard for me to set up an experiment that demonstrated the emission of gray light. Why? Light, when taken in isolation, can never be gray. We only see gray when it is viewed in contrast to another brighter, whiter color.

Just plain stupid

Just in case you were hoping for another blog post about stupid memes, I can top those last few blogposts!