Unambiguous regions in color space for the basic chromatic colors

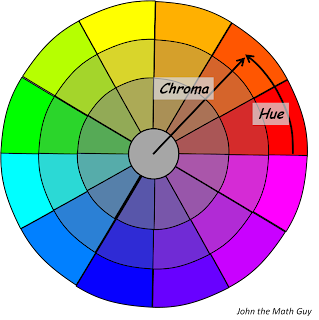
I am going to start this blog post with the punchline. The image below shows the range in color space of the eight basic chromatic colors. I assert that any color that is within a given set of limits will be unambiguously identified by the corresponding color name by everyone except for people who are either Color Vision Deficient (CVD) or Color Naming Pretentious (CNP). 

If a color is in one of these regions, then it has an unambiguous name!

Note that this is an a*b* plot. Each color also has a viable range for L*. Stick around for the end of this post, and I will provide a simple mathematical description of these regions -- but that's a treat reserved for those people who read through this entire blog post!

Why is this important?

Before I go any further, I have a confession to make. I write this blog post (and put all that time into the data analysis) in hopes that I will someday win this running argument that I have with my wife. I know. Good luck, John. I can dream, can't I?

Here is how the argument typically plays out...

Math Guy: Did you see that woman with the gorgeous brown hair? She just winked at me and smiled. I'm gonna go ask her for her number.

Honey, she smiled at me!

Bride of Math Guy: Don't be such a dufus! Her hair is auburn, not brown! 

Math Guy: But, Honey! I know color. I am a color scientist!

Bride of Math Guy: That may be, but you're still wrong.

If only I could walk over to the brunette (who is obviously attracted to immensely intelligent guys like me), ask to measure her hair with the spectrophotometer that I always carry in my pocket, and then bring up a ColorNamer app to give me the unambiguous name for the color of her hair. If nothing else, you gotta admit that this is a novel pick-up line. And just maybe, it could be used to avoid marital strife.

If you have doubts about the importance of the question of color naming, witness the following. There is a prominent, well-respected, and humble color scientist/blogger who has devoted no less than six blog posts to the topic of assigning names to colors.

What color is red?

Is my green the same as yours, revisited

The definition of vermillion

The Joy of vermillion, take 2

Arranging paint and (once again) vermillion

What color is the dress?

I dunno, maybe the name of a color is important for other reasons. I mean, there are a few odd cases where words are used to convey information, and the color associated might be important to somebody.

My data

I recently ran into a pile of papers written by Dimitris Mylonas. Unlike me, he has been doing a lot of real research. His research topic for his doctorate at University College London has been how people assign names to colors. He has been running an online experiment where he displays colors right on your own computer and then asks you to name the color. He has made the results available through an online color naming app where you can select from 30 color names and it will display the most common color associated with that name. Or, the other way around, you can click on a color from a palette, and you will get a word cloud with the most common names that your RGB combination has been given. Great entertainment for a rainy day. I gave up my subscription to Netflix when I found this.

Screen capture from Mylonas' site

There was a similar color naming experiment that was conducted by Nathan Moroney of HP. You can get a free copy of his color thesaurus online.

Snippet from Moroney's book

For both of these sources (the online app from Mylonas and the book from Moroney), I harvested RGB values for each of the basic chromatic color names: red, orange, yellow, green, blue, purple, pink, and brown.

Why these colors? 

Why not beige, turquoise, plum, coral, lilac, etc?

I do have some logical foundation for the colors I chose. It is based on a seminal paper in the study of chromolinguists by Berlin and Kay in 1969. They did linguistic studies of color names in eleventy-seven zillion different languages and came to the following conclusion:

"... a total basic inventory of eleven basic color categories exists from which the eleven or fewer basic color terms of any given language are always drawn. The eleven basic color categories are white, black, red, green, yellow, blue, brown, purple, pink, orange, and grey."

The eleven basic color categories

I think that's pretty amazing. There are many independent roots of languages, and for some reason, they eventually all settle on eleven words for basic color names. The words are different, of course, but they all kinda translate. You don't run into a basic color word in Swahili that translates into "a sorta brownish shade of red, but not so dark". There must be something fundamental to the human eye or the neural pathway to the human brain that segregates color into these eleven groups.

I should mention here that the bulk of the Berlin and Kay paper dealt with a recurring pattern in the development of languages. They posited that nascent languages include white and black in their vocabulary, later adopt a name for red, then either yellow or green, followed by green or yellow, etc. The sequence up to these eleven colors is largely predictable.

There has been much research based on the work of Berlin and Kay, and it mostly supports the eleven-ness of color categories. Perhaps there are a few colors (such as beige, turquoise, plum, and coral) that belong on the next tier, but these are clearly the Magnificent Eleven.

In the old west, life was lived in black and white,
and there were only seven magnificent basic colors

I did a little tiny bit of research on this topic. Years ago, I taught algebra to people who hated math for University of Wisconsin Milwaukee. One semester I had about 50 students, half male and half female. I asked them to write down all of the single-word color names they could think of, and gave them two minutes. 

There were perhaps three or four lists that had only ten of the Magnificent Eleven, but almost every student had included the eleven basic color terms. The next two color names in terms of frequency, were silver and gold, which each appeared on about half of the lists. That in itself I found interesting, since as a color scientist, I know that silver and gold are gonio-apparent effects, and not actually colors.

My paltry little experiment demonstrated once again that there is something magical about these eleven colors.

So, for this experiment today, I decided to go with that set of eleven. But I left off the achromatic colors (white, black, and gray) due to some technical problems beyond my control. I didn't think that neutral colors were pretty enough.

A caveat

There is always a caveat, isn't there? These two online experiments are absolutely fabulous work. Incredible amounts of data. In one of his papers, Mylonas states that there had been over 1,400 participants in his experiment, Moroney claims over 5,000. 

Here's the caveat, though. You can bet that most of the computer displays were uncalibrated. There were certainly 6,400 different viewing conditions, if you consider intensity and white point of the display, ambient light, and background. So when Sidney from Sidney looked at a shade of lime green that was created by the RGB values 30, 230, 40, and Charlotte from Charlotte viewed that same combination on her monitor, there is apt to be a difference in what they are actually seeing. Anyone who has used a laptop with a second monitor can appreciate this issue. 

So, we identify that this is a source of experimental variation. We have literally scads of data, but are unsure about the quality of the data. But, I used it for my experiment anyway. I'm not proud.

Both researchers provided us only with RGB values associated with the color names. Before I go on, I should explain that "RGB" is not a standard. It could refer to any of the particular flavors of RGB values associated with whatever monitor or cellphone or camera you are using. But adding an s to the front of RGB wildly changes the connotation of the whole thing in much the same way that adding a little s does to your ex. sRGB is a unique standard that can be converted into the standard L*a*b* values. That would be a handy trick right now.

I asked my good buddy Dimitris Mylonas if it would be reasonable to assume that his RGB values were sRGB. I could almost hear him shrugging his shoulders through the email: "sRGB is safer than any other assumption." So, I used the standard computation to convert from sRGB to L*a*b*. Here is a website to do the conversion from sRGB to L*a*b*.

An obvious question here

I can see one of you bouncing up and down with your hand in the air... yes? You want to know whether the two data sets agree with each other? Good question! I wish I'da thought to do that! 

In the graph below, the circles represent the Mylonas data, and the squares with an outline represent the Moroney data.

Comparison of two versions of the basic colors

So, the answer is no. They don't match. The color difference ranges from 12.5 DE_ab to 46.4 DE_ab. Not good matches by any stretch of the imagination. There is a consistent pattern, however. The Moroney data is always more saturated. And the two data sets have very similar hue angles. With the exception of yellow and blue, the hue angles are all within 4˚ of each other. 

I don't have a ready explanation for why the two experiments differed so much. Given the size of the data sets, the difference is due to some sort of bias between the two experiments, and is not a statistical anomaly. If nothing else, this is a caution for this endeavor: If we try to precisely define colors, there be dragons.

The eight color map problem

So here I am: I have L*a*b* values for the eight basic chromatic colors, but, truth be told, these numbers have somewhat of a checkered past.

Enter Sturges and Whitfield

If only I had some data that was taken under standardized conditions. Even if it were to be done with less than a cast of thousands, if it corroborated the online studies, then the online studies would be corroborated.  The good news is that such a study was done in 1995 by Sturges and Whitfield. They elicited the help of twenty students at their university in England. Half were male and half female. None had any specialized training in color, err, excuse me, in colour.

The experimenters selected 446 color chips from the Munsell Book, and asked each subject to give a monolexic name for the color of the chip. (From mono, meaning "the kissing disease", and lexic meaning "someone who can't remember the first three letters of their learning disorder", monolexic means "single word". Hence pink, aubergine, and sploofrinde are all monolexic. Burnt sienna and reddish-green, are not monolexic. Owyell, by the way, is dyslexic, and there are no English words that rhyme with orange. Except for sporange, which means "word that rhymes with orange".

Did I mention? Twenty subjects named 446 randomly ordered patches, and I forgot to mention that they were given each patch twice.

S&W thus had a lot of data to distill down -- about 18,000 words. Among other things, they tried using consensus to decide when a given name was proper for a given patch. If all twenty trials on a given patch yielded the same name, then there was consensus. I was a bit surprised but even with this stringent test, there were 102 patches where there was a consensus as to the name. For about one-quarter of the patches, twenty people independently came to the same conclusion about the monolexic name.

So, my third data set was this set of 102 colors and their associated names. Since the colors were reported in Munsell notation, I used the Munsell renotation data to convert to L*a*b*.

Am I done yet?

Just to be safe, I wanted to throw in a few more data sets. I happened to have measurements from a Macbeth Color Checker chart. (This shows my age. People who don't immediately recognize the names "John, Paul, George, and Ringo" will know the Color Checker by the name X-Rite Color Checker.) This chart unfortunately does not include pink or brown.

And I did wy own color naming experiment. I tossed a Pantone book at my wife and asked her to find the best representation of each of the basic color names in the book. Her brother, who is also color-savvy, was given the same test, and I recorded my answers as well. (In case you were wondering, we disagreed on pretty much all of them.)

Here are the results for the color purple. Each dot represents a "sample". Thus, the 5,000 people who took the Moroney test get one circle. The twenty college students who spent the better part of a weekend staring crossed-eyed at Munsell chips instead of going out to a proper pub got a total of fourteen circles -- one for each Munsell patch that they all agreed was pruple purple. And I got one circle all to myself. And, begrudgingly, I gave one circle to my wife and brother-in-law as well. Life isn't always fair. If one of the people who took the Mylonas test wants more than 1/1,400th of a circle, they can get write their own darn blog post.

The X in the middle is the average of all the data.

The range of the color purple

Looking at the scatter of points of purple and of other colors, I saw a shape that was bounded on two sides by two hue angles, on two other sides by two chroma values, and (not shown) bounded on top and bottom by two L* values. Since I had some clear outliers, I let Excel tell me the 10th percentile and 90th percentile of  L*, C*, and h.

Note: I had originally called this last one H*. Thank you Tammo for the correction!

Results, in graphical form and numeric form

The graph below may look familiar to those who bothered to read the first part of this blog, and who were also paying attention. It is the same graph as above, meticulously duplicated for the benefit of my dear readers.

Partitioning of color space into base color names

	Low L*	High L*	Low C*	High C*	Low h	High h
Red	41	49	59	86	27	37
Orange	62	72	67	96	57	67
Yellow	81	90	68	109	86	97
Green	31	72	29	80	122	168
Blue	31	71	24	58	-112	-71
Purple	25	52	26	81	-56	-35
Pink	62	81	25	54	-23	21
Brown	29	41	26	43	55	76

Let me know if you find some use for this. I found some use... I wrote a blog post, and looking at this graph gives me a bunch of ideas for future blogposts.

Organizing your crayons

My little buddy here is intent on an important task. He is trying to organize his crayons.

Go ahead, make my gray!

You may think this is an easy task, organizing crayons, but you would be wrong. At least, that is, if you are an adult. I distributed crayons to a group of first and second graders. I set them loose in a gym and asked them to organize themselves by color. It took maybe ten or fifteen minutes, but they did it. I gave the same task to a group of managers in a large corporation that shall go nameless. They held preliminary meetings with action items for subcommittees to perform market analysis, develop a business case, and research environmental impacts. Project leaders were appointed to develop realistic estimates of timelines, and to do risk analysis. I expect them to get back to me  by mid-June with a detailed action plan. They got started back in September of 2007.

Arranging crayons in a line

One possible way to arrange crayons is by the colors of the rainbow. I pulled 13 crayons out of my favorite box of crayons and made a nice lineup which I call the "craynbow" [1]. You can see red, red-orange, orange-red, orange, yellow-orange, orange-yellow, yellow, and so on.

The craynbow

I know this is completely atypical of me, but I sort of told a lie. The last two crayons on the top, the red-violet and violet-red, are not actually in the rainbow. The most startling difference between the rainbow and the craynbow is that the rainbow is two crayons short of a full deck. This is probably obvious, but the additional two crayons form a bridge that allows us to connect the bottom of the craynbow to the top. Thus, the 13 crayons can be laid out in a circle. 

But there are just a few other crayons that didn't make the cut. Most notably, the craynbow is missing white, gray, black, pink, and brown. Also the craynbow does not have a spot for lavender, burnt sienna, periwinkle, or maroon [2]. There are 96 crayons in my box, and 83 of them don't have a spot reserved for them in the craynbow. You don't have to be the sharpest crayon in the shed to see that you can't arrange a box of crayons in a single line in a way that chromatically feels good [3].

Color is three-dimensional

There is a simple reason why we can't put all the colors in a line. Color is three-dimensional. The craynbow looks at just one of those three dimensions of color, that is, the hue. Us color theory guys have two additional attributes that we assign to colors: chroma and lightness.

Showing hue and chroma

Let's start out with those 12 crayons arranged around in a circle. (I don't know what happened to the 13th crayon, by the way. Maybe it fell behind the couch.) What happens if we mix each of those crayons with a little gray, and then with a lot of gray? The results are shown in the really nifty circle below. Feel free to drop the artist an email telling him just how much you like the circle.

This cool drawing took me four hours to draw

Now for the cool part. Any color in this circle can be identified by naming the hue (the original crayon) and the chroma (how far it is from gray). The hue in this circle is the crayon that you started with. The chroma tells us how much gray was mixed in, that is, how rich the color is.

By the way, if you happen to be into analytic geometry, you might realize that hue and chroma are polar coordinates for the color plane. If, on the other hand, you don't really care all that much about anal retentive geometry, then you probably don't care about whether your polars coordinate.

Showing lightness and chroma

This next image demonstrates how lightness (along the up and down axis) combines with chroma (along the right to left axis). All the colors in this image have the same hue, yellow-red (5YR) [4].

A page from the "Munsell HVC Color Charts"
(It took me four hours to put these paint chips in order.)

Along the left edge, we see a scale of colors that go from black up to white, all with just a tiny bit of orange flavoring to them. As we move to the right, there is more and more orange added--that is higher chroma.

Notice that we just don't get all that many shades of orange-black. As you add orange (or yellow) to black, it just has to get lighter. Thus, there is only one shade of orange on the bottom row. On the other hand, you can add orange to white without significantly decreasing its lightness. So, there are four shades of orange in the top row. The most saturated orange is basically still a pretty bright color. Blue and purple work pretty much the opposite way. Adding blue or purple to a pale gray will necessarily make it darker. It is possible to have a very saturated blue or purple that is also very dark.

These three attributes can be put together to create a color tree. The pages (like the one above called 5YR) are bound together at the left edge, and fanned out as shown in the very detailed and elaborate illustration below.

Here is another four hours of my life spent in Photoshop

Such a color tree was devised by Albert Munsell in the early 1900s. It is a testament to his genius and meticulousness that you can still buy a facsimile of this color tree almost a full century later. Not only that, but the guy actually has a blog, despite the fact that he died in 1918. He must be a ghost writer, I guess.

A very attractive model shows the Munsell color tree

Someday I will write a blog post about how this guy Munsell laid the foundation for the ever-popular color space CIELAB, and came to be known as the Father of Color Science. He was also the father of A. E. O. Munsell, who carried on his work. I don't intend to write a blog post about how Albert became the father of A. E. O.  

What this all means

The first message is that you need three dimensions to organize a box of crayons. That's cool, but the more important message is that with the colors organized and quantified like this, it is possible to put a unique identifier on each color. All you need to do is specify the hue, chroma, and lightness, and you can unambiguously label any color. This might not be as romantic as using words like vermilion or aubergine, but it's a darn sight more precise. What young lady wouldn't prefer to hear poetry that scientifically specifies the color of her rosy cheeks?

  

----------------------------

[1]  A major supercomputer company is developing a computer just to compute all the colors in the universe. The computer will be called the Cray-Ola.

[2]  A ship loaded with red paint collided with a ship loaded with blue paint. All the crew were marooned.

[3] I used to tell my color classes just that you can't arrange your crayons all in a line in a way that made sense. Some smart alec said "Sure you can. Alphabetically!"

[4] I understand that some people might be so silly as to call the color "5YR" by the pedestrian name "orange". Please try not to laugh at them, ok? (My wife told me that I should point out that I'm being sarcastic here.)

How many colors are there - Addendum

I am reminded today of a line from the song "Alice's Restaurant Masacree" by Arlo Guthrie. He and his friends were off to the garbage dump on Thanksgiving day, when they found the dump closed. Here Arlo takes over the narrative

... we drove off into the sunset looking for another place to put the garbage. We didn't find one. Until we came to a side road, and off the side of the side road there was another fifteen foot cliff and at the bottom of the cliff there was another pile of garbage. And we decided that one big pile is better than two little piles, and rather than bring that one up we decided to throw our's down.

I am quite happy about all the responses I have had to my post on counting the number of colors, ranging from the highly technical to the downright flippant. These responses were posted in a variety of places, and I have decided that one big list of comments is better than five different small lists of comments.

Here's how others answered the question of how many colors there are.

My co-worker Parker Will, who always cracks me up, sent me a link to one person's very imaginative answer. 512 cubic inches. This book simply contains all the colors that are fit to print. It reminds me of a book that may still be in my basement... a book which is a times table from 1 to 999 by 1 to 999.

The RGB Colorspace Atlas

Here are some answers from various LinkedIn groups. I have added some of my own snarky comments.

Nancy Eagan ...as much as there is sunlight ..?

Wei Ji • I think the ultimate question is: how to define "a" colour? the unit that enables us to count how many colours are there.

[Me - Excellent point!]


Mark Taylor • Very thoughtful article. You missed "4" - which is the answer an inkjet printer would give you ;-) 

By the way I've also wondered about what the limits of CIELAB space were, and just assumed as a self-taught color scientist I hadn't yet read the right book!


Gary Field - Research on the number of colors issue usually starts with reference to the Dorothy Nickerson and Sidney Newhall paper of 1943 (JOSA, pp. 419-422). They conclude that there are about 7,500,000 surface colors at "supraliminal" viewing conditions, and 1,875,000 colors when viewing conditions approximate those used for color matching work.

Some experimental work of mine (1996 TAGA Proceedings, pp. 14-25) from a printing industry perspective suggested that the offset lithographic process could produce about 1,200,000 colors, while the gravure process could achieve about 1,500,000. A later estimate by Andreas Paul of FOGRA was about 1,000,000 colors for 4-color offset lithography, and around 1,400,000 for seven-color lithography.

Mike Pointer and Geoff Attridge concluded that there were about 2,280,000 discernible colors in their 1998 CR&A article (pp. 52-54).

A "color" could be said to exist when an observer indicates that the perceived new sensation differs from a previous sensation. The "16.7 million colors" touted for color monitors means, in my opinion, that there are 16.7 million different combinations of RGB radiation, but because many of these combinations are visually identical, they are not distinct colors from a human perspective. The estimates reported in previous paragraphs are based upon color difference equations of one type or other. Different equations will produce different results, and the illumination level exerts a powerful influence upon the visual color discrimination task.

A TAGA essay of mine, with more detail and some extra references, entitled "The number of printable colors" appears in a collection published under the title of "Color Essentials - Volume 2" that was published by the Printing Industries of America.

http://store.piworld.com/store/p/120-Color-Essentials-Volume-2.aspx

[Me - I am honored to have you comment, Gary. I have one of your books in my bookcase! I have read through your paper, Gary. If I understand correctly, the number is more or less based on the original deltaE formula? Better estimates could be arrived at through DE2000, although this would be a lot of work. I agree with your assessment of the 16.7 million number.]

David Albrecht - There are 4 million colors, give or take a few. This is based on the observations and surveys done over the years for a trained human eye and what it can observe. As Gary points out, a monitor may be able to display more combinations of RGB, but we will only be able to see about 1/4 of the combinations. And according to the rules of observation, if we can't observe them, they do not exist. The "if a tree falls in the woods" concept.

From this 4M or so we drop to untrained human eye, to "compromised" human eye (color blind/deficient), printable colors, etc. It's still amazing that we can reproduce those 1M colors with just 4!

[Me - Nice to have a comment from an old friend.  If a color falls in the woods, will someone walk by and return it to the box?]

Gary Field • Adding to David's comment, color discrimination capability for those with normal color vision peaks between the late teens and early 20s. This brings to mind Keith McLaren's observation concerning "correct" color vision; it is "... always that of the observer having the power to accept the batch as a good commercial match". 

So, the young do indeed have a more colorful world, but the older people who usually wield the 'OK' stamp of approval, establish the color boundaries.

Alessandro Rizzi • Let me suggest an interesting paper about the impossibility of counting the number of colors:
"Why we don’t know how many colors there are"
by Ján Morovic, Vien Cheung, and Peter Morovic
presented at CGIV 2012 conference this year
http://www.slideshare.net/jmorovic/why-we-dont-know-how-many-colors-there-are

Gary Field • @Alessandro: Thank you for that link to the CGIV paper about why we don't know how many colors there are; I found the authors' slide presentation online. Except for very constrained conditions (observer, viewing source; or, if computed, the formula), a definitive, universal number is not likely. I will be happy when claims of "billions" or "a few thousand" colors no longer appear in print (yes, a low bar!).


Arnaud Fabre • Everybody agrees on the fact that the conditions to compute the number of colors are : 
- a well defined set of observation conditions 
- a perceptually homogeneous colorimetric space 
I did not read the paper of CGIV, but I assume that it only ask how we can do serious science with at the basis a vision test applied to 30 persons more or less. And of course Lab is not so perceptually homogeneous, and even with the dE2000 patch, the parameters and the threshold are not so obvious to set. 
But it is the only thing we have, right ? and it did not work so bad most of the time. So the basic idea is more : 
"how can we compute the number of color that are available with those assumptions ?"


Paul Lindström • John – on DE2000 – What is commonly repeated is that a DE of 1 when using the DE Lab formula from 1976, is a reasonable threshold for where humans with reasonable colour vision see a difference between hue shades (colours). When using DE2000 my guess is that the threshold should be somewhere be between 0.5 and 0.75. Might not sound much of a difference, but using 0.5 would double the number of colours (if my layman use of math is correct).

[Me - Math Guy time... if 0.5 DE were to be used instead of 1.0 DE, the number of colors would go up by a factor of 8, since there would be twice as many in all three directions.]

Ryan Stanley • John,

I noticed that in this question vs. your blog you phrase the question two ways:
1: How many colors are there?
2: How many colors are in your rainbow?
The way you interpret those questions can give different answers. Further I think this is where confusion in the industry comes; from laymen to scientist.
I say this because the first question is more scientific; how many colors are there…actually?
For this discussion, let’s look at the “reflectance curve” of light or what “makes” our color as a guide.
If we use what has been defined as the “visible spectrum” of electromagnetic radiation, we find ourselves roughly between 380nm-700nm. Over the years we’ve had spectrophotometers break this down for us with % reflectance across this band. Leaving out fluorescents for this exercise and saying that 0% reflectance is absolute Black (absence of light) and 100% is absolute White (all light). The earlier models commercially available could read every 20nm; now we have models widely available that ready every 10nm; newer models becoming available that can read every 5nm. But let’s just say every 1nm; for if there is a difference in reflectance then there is a difference in color (were not talking about perceivable color just yet).
That’s means from 380 to 700 we have 321 distinct points available for our reflectance curve across the visible spectrum.
Each point has the potential to reflect all light 100% or no light 0%, as well as all points in-between; leaving out decimals for simplicity’s sake (we should measure out to at least two however 000.00) that gives us at least 101 points to choose from.
So we find our % reflectance or “n” is the number of things to choose from, and we choose 321 of them or “r”. With order not being important, and repetition allowing, we have our formula for “how many colors are there?”:
(n+r-1)!/r!(n-1)!
The answer is striking, so I’ll give the short one: 7.83532204e+98
-This is roughly (we only used 0%-100% as whole values) how many colors are available in the visible spectrum for us “to be able” to perceive.

The next question is ambiguous; “how many color are in your rainbow”, or how I read it; how many colors can you see?
You showed a chromaticity diagram in your blog, with that as a reference;
The way humans perceive light can be compared to how we engineer color as well. We have rods, cones, and available “opsins” (light sensitive chemicals) in our eyes that allow us to perceive shades. This is inverse but still comparable to the Red, Green, and Blue LED’s that make up our computer monitors, or the CMYK pigments in our printers. In the diagram you show what we can see vs. what we can produce or what’s in or out of gamut.
Similar to how you mention “it is impossible to build a computer monitor with three fixed lights that will display all possible colors” , it is additionally impossible for the opsins in our eyes to “perceive” all colors that are available to “receive”.
So depending on who you are, how old you are, your gender, race, which eye you use and even what species you are we all “perceive” color differently. This is what makes color so hotly debated and unique! There are even tetrachromats, or women who can see FOUR distinct ranges of color; making their world much more rich I can imagine.
This is the number where no one really has the right answer and as you state in your blog: “Pick a number between 3 and 16,777,216” .

I would be curious to know if anyone has performed a study or has information on the ability of the opsins to receive light at various levels?
This would allow us to create a similar chromaticity diagram for what we “should” be able to perceive vs. what is available to receive.
Interesting topic; I look forward to other responses.
-Ryan Stanley

[Me - I am going to disagree a little bit, Ryan, on a semantic basis, with your scientific answer. It comes down to what the word "color" means. I think the definition that you have given is something like "unique spectral stimulus". If you go down this path, then I think the number you should come up with is a zillion to the zillionth power, since each of the zillion photons received by the eye could have any of the zillion available wavelengths. But, I don't think it's fair to call each unique spectra a "color". Color does not occur at least until the photons enter the eye. This is, of course, semantics.]

Amrit Bindra • There are as many colors as one could perceive or as a community we all could jointly perceive.

Gary Reif • This is all a reminder that we live in an analog world.

George Dubois -  If you go by the L,a*,b* color sphere where virtually all colors go from a= -60 to +60 and b=-60 to +60 and L goes from 0 to 100 then you have a color space of 1.13 E 6 (1,130,000). If taking a Delta E for most people of 1.0 being distinguishable then there are 1.13 million colors. If you prefer to say that good people can see to .5 Delta E then the number would be 4.5 m.

[Me - This is a quite reasonable "back of the napkin" estimation. You have assumed a cylinder with average radius of 60... ehhh... sounds good. The choice between cube, cylinder and ellipsoid would give a range between 0.7 and 1.4 million. The assumption that 1 deltaE (or 0.5 deltaE) is the limit of human perceptibility is a bit more iffy, I think. A change of 5 delta E in the chroma of bright yellow is barely perceptible, whereas a change od 0.5 deltaE near gray is barely perceptible.]   

Ryan Stanley • As with all topics concerning color or colour, it can be debated to include a greater portion of the UV and IR portion of the spectrum (why i stated roughly) as 380-700 is more universally accepted. To your point however, if we expand it out further and add 20nm on each end, we only find ourselves with an even larger number of potential colors available to receive.
In reference to "how many NM are there between viable differences" I would ask;
what is the definition of viable in this case, or what are you looking to achieve?
Further to the point, "do we get too complex abou how we look at colour?" And bringing both topics together, I would say;

Color and the science of color or more succinctly the interaction between matter and radiated energy is so much more than just what we can see. From instruments that can tell us what metals we have in seconds to unlocking the composition of the atmosphere on a planet in another solar system. We've even been able to identify the expanse of the universe through Doppler or the red/blue shift of distant stars. All through our understanding of "Light".
Armed with the knowledge of color, we begin to use it and shine that light back on the mysteries of the universe. Only through a complex walk can we arrive at simplicities door.
To quote Albert Einstein:
"A man should look for what is, and not for what he thinks should be",
"The most beautiful thing we can experience is the mysterious. It is the source of all true art and science."

Interesting topic; I look forward to other responses.
-Ryan Stanley

[Me - Here are the other responses, Ryan! Thanks for the suggestion.]

John Wells • But if you are colour blind, how many colours can you see? I have seen colours matched to less than 0.5 dE and would say they do not match! The colour matchers eye is critical. The analog version is merely a tool to aid those with less critical vision and to overcome the human foibles. For instance put two similar colours side by side, after about 30 seconds the brain, which does not like differences, will try and merge the colours, hence some colour matches are worse than others. The human eye is king (So long as you are not colour blind) and all following analog based matchings, should be based on the total conditions observed at the time the eye passed the colour.

[Me - If someone is colorblind, the number drops appreciably, since color space is two dimensional or one dimensional. As for discerning changes of 0.5 deltaE, that points out a problem with deltaE 76.]

[Me - This one below was my favorite. It was posted on the blog itself. Anyone who knew me in my previous incarnation as John the Revelator knows that music has always been a big part of my life.]

Steve Fowler
we need look no further than Joseph and the amazing technicolor dreamcoat.
the answer is clearly 29 (or maybe 27, or 26 if you're an art teacher).
red and yellow and green and brown and
Scarlet and black and ochre and peach
And ruby and olive and violet and fawn
And lilac and gold and chocolate and mauve
And cream and crimson and silver and rose
And azure and lemon and russet and grey
And purple and white and pink and orange
And blue
Newton, phah...Tim Rice and Andrew Lloyd Webber have the answers (except for silver and gold.....oh yeah, and black)

How many colors are in your rainbow?

“Ok, mister smarty-pants Math Guy who thinks he’s a color scientist, answer me this!  Just how many colors are there? Huh?”  I get that question all the time. Boy have I got an answer for you. Or maybe a whole bunch bunch of answers…

This blog is dedicated to Jerry Nelson, the voice of The Count from Sesame Street. Jerry died August 23, 2012.

The Count

Three

The simplest answer is that there are three colors: red, green, and blue.

On the off chance that you don’t believe me (maybe you were gonna say there are more?) pull out a magnifying glass, or a microscope, and look at your computer monitor. Unless you happened to grab a scanning electron microscope[1], you probably see something like the image below. Your computer screen is a combination of red, green, and blue dots. Every color that you can see on your screen is a combination of those three colors.

Picture of red, green, and blue pixels on a computer screen

For the sake of honesty, I have to say that this last part was something of a lie. Not really a lie, but perhaps misleading – like telling your wife that you are out with “the guys”. The thing is, you can’t get every possible color on your computer monitor. You can get a whole bunch of them, but have a look at the chromaticity diagram[2] below.

The chromaticity diagram, showing the gamut of a hypothetical computer monitor

The black triangle shows a hypothetical gamut for a computer monitor. The three vertices of the triangle represent the colors of the red, green, and blue pixels. By mixing the colors, you can reach any color within the triangle.

You will note that there are colors that are outside the gamut of this hypothetical monitor. In fact, it is impossible to build a computer monitor with three fixed lights that will display all possible colors. Chromaticity space is bowed out, so you can’t make a triangle with physically realizable colors (colors within the horseshoe shape) that covers all possible colors[3].

Here’s another fun experiment. Go into Photoshop or Paint or whatever program that allows you to select colors. Try to make orange. Not only can’t you find a word to rhyme with orange, but you can’t make a good orange on a computer monitor[4]. The best I could do looks a little brownish.

The best orange I can make on my monitor (RGB = 255, 192, 0)

So, my first answer to the question is that you can make good percentage of all possible colors out of just three colors. Four colors might be a bit better.

Seven

How about the number of colors in the rainbow? The colors from the rainbow can be combined to make every possible color. Isaac Newton did some research with prisms and sunlight, and decided there were seven colors in the rainbow: red, orange, yellow, green, blue, indigo, and violet (ROYGBIV). The other colors I get, but what about indigo? I’m not sure I even know what indigo is!

Here is my explanation of how indigo got into the rainbow. Newton saw a big section in the blue that seemed just too wide to be a single color. Now, Newton was something of a mystic, so he saw a fundamental connection between the seven elements, the seven planets, the seven notes of the tone scale on the piano, and the seven colors of the rainbow.

Or maybe he looked at the color just below 500 nanometers, and rather than call it light blue or cyan, he decide that was blue. Having no other name, he was forced to use indigo to name the color that I might call blue or possibly dark blue. This is at least plausible, since the word “cyan” didn’t come into use in the English language until 1879.

My second answer to the question of how many colors there are is seven, or maybe six.

Sixteen million

Now I’m going to go to the other extreme, and claim that there are 16,777,216 colors, and that my computer monitor can prove it. Those of you who recognize this number as 256 X 256 X 256, will immediately understand that this is the number of RGB combinations you get when you have 256 levels of red, and 256 levels of green, and 256 levels of blue. If you do not recognize this number I’m sorry, but you are a poor excuse for a computer geek.

Just because I can go into Photoshop and make 16 millions colors, does that mean there are really that many colors? The image below might persuade you that there are (possibly) not that many. One of the rectangles has the RGB values 255, 255, 255. The other has the RGB values 254, 254, 254. I don’t know what you see on your screen, but I can’t really tell the difference.

In other words, while there are 16 million possible combinations of RGB, not all of them are distinct “colors” according to the eye.

Which rectangle is brighter?

My third answer is that there are 16 million colors on my computer display, but that might be a little bit of computer hype.

Eleven

I taught an algebra class at UW Milwaukee. One day I gave a pop quiz to my two classes. I asked them to take out a sheet of paper and a writing implement. I gave them two minutes and asked them to write down all the single-word color names that they could think of.

The eleven colors that everyone can think of

I had 50 students that took the quiz, half male and half female. Almost everyone – 48 of the students – came up with the names of the eleven colors in the picture above: white, black, gray, red, orange, yellow, blue, pink, brown, and purple. If I remember correctly, there were two students who said that their art teacher told them that black is not a color; it is the absence of light. So that explains that. What do art teachers know?

The next two colors down the list were silver and gold, each with about half of the students recalling those colors. I am going to argue with the art teacher that silver and gold are not true colors. They are gonio-apparent effects. And I am right, since this is my blog.

So, my fourth answer is that there are eleven basic colors that everyone can recall.

An interesting thing showed up in the data. There was a statistically significant difference between the number of colors that the men could recall versus the number that the women could recall. Men averaged 15, and women averaged 18. Not a big difference, but my sample was wide enough that it was significant. Now, it could be that my sample was not representative of the population since there is a bit of a gender difference in math performance and this was an introductory algebra class taught in a college. OR it could be that women are inherently more color conscious. I have no real explanation, other than stating what I observed.

The student with the most colors was a female art student, who recalled 29 colors in the two minutes allotted. I have given this test to a number of other times, in particular, to my wife. In two minutes, she was able to recall over 50 single word color names. After the two minutes were up, she kept writing down single word color names for a few hours after, eventually compiling a list of nearly 250. Can there be any question about why I fell in love with this woman?

Answer number five: there are somewhere around 250 colors that my wife can name.

Something like fifteen

I performed another experiment, this time on myself. Unlike many of my other experiments, this one did not involve mind-altering chemicals. It involved colors. I started with a big bucket of possible colors, and tried to assign each of these to a color family. I started with the eleven basic colors as my names for color families.

There were a lot of colors that fit in more than one family. For example, yellowish orange belongs in both the yellow and the orange families. And reddish green fits into both red and green[5].

As I went through my bucket of colors, I came up with a few sets of colors where I wasn’t comfortable with putting the color in any of the families. One group could be called beige, taupe, off-white, or possibly eggshell. These were colors that were really not white, but they were not saturated or dark enough to be called brown or yellow. Another misfit color was tan. Is it brown, or yellow? Not really either, I think. Or maybe it’s really brown.

Another group that didn’t seem to have a proper color family included the colors coral and fuchsia. Were these red, or orange, or maybe pink? I couldn’t decide. Maybe it is in the purple family? Nothing seemed to fit

And then there was plum or burgundy, kind of a brownish dark purple. Maybe sea foam was another group, and that group might include the color that my wife argues with me about. Cyan, turquoise, aqua, powder blue, sky blue, teal, periwinkle, azure, cerulean… (Are you kidding?!?!??  Periwinkle doesn’t belong with those colors!)

I count three or four or maybe five additional color families, so my sixth answer is that the total number of color families is around fifteen. But, I have no idea what a different observer might say. I hesitate to run this experiment on my wife.

One hundred fifty or two thousand

It wasn’t that long ago that the biggest box of Crayola crayons available (with 96 crayons) was proudly displayed on my desk. Today, I see that you can buy a set of 150 crayons for the low price of $14.97. A must have for any serious color scientist. My birthday is coming up, by the way.

Crayola 150-Count Telescoping Crayon Tower

Crayola is not the only company that is compelled to add more colors. Pantone just recently announced the addition of 336 colors to their color formula guides, bringing them up to “1,677 chromatically arranged color choices to unleash their passion and let their creativity soar.” I heard many passions unleashed by printers at the necessity to drop another $100 on their color matching books.

Not to be outdone, the Valspar American Tradition paint swatch book has 1,764 colors, including “Homestead Resort Parlour Raspberry”, “Misty Morning Blue”, and the very popular “Swampwater”. Swampwaters were very popular when I was in college. No one knew what went into them.

So, the number of commercially distinguishable colors is somewhere between 150 and 2,000. My seventh answer to the question.

Two million

Now we get to some more scientific answers. Let me make the question a bit more precise. How many distinct colors can be reliably distinguished by people with normal color vision?

The quick and dirty answer comes from looking at the bounds of CIELAB space[6]. CIELAB space was designed so that one step in any direction is approximately “just noticeable”. The value of the lightness value goes from 0 to 100. In the red to green direction there are let’s see, how many steps? Lemme check my copy of Wysczecki and Stiles. Hang on a sec… Still looking…

Ok, so they don’t say how big color space is in that direction. Or in the blue to yellow direction. Let’s just assume that there are something like 200 steps in each direction. That means that the rectangle that fits all of color space is 100 X 200 X 200, or about four million.

Of course, this assumes that color space is a box-shape (rectangular prism). But color space is not rectangular. Maybe it’s more like an ellipsoid? My buddy Adam has referred to the shape as a “space potato”. Let’s just say that it’s an ellipsoid, in which case, the volume is about half of the volume of the box, or two million. Answer number eight.

Some other number?

How many lies have I told so far? Well, I need to admit to another one, or at least another misleading statement. (Honest, I was out with the guys that night.) I said that “CIELAB space was designed so that one step in any direction is approximately just noticeable.” I did put the word “designed” in italics to tip off that this might be a white lie.

I have to admit that, yes, this was the design goal, but it is not really all that exact. For example, if you take five steps in the direction from saturated yellow to really saturated yellow, you will just barely be able to tell the difference in color. On the other hand, if you have a color near gray, you can get away with only about half a step before you can see a difference.

This means that the reconnoitering in that last section is a bit flawed. What’s the real number? I honestly don’t know. I have some ideas on how to compute it, though. I do know that there are only about 70 steps in the lightness direction, whereas CIELAB says there are 100.

My ninth and final answer: Someday I will actually write some code to figger it out, but I suspect the number of discernible colors is around 689,262. Then again, maybe it’s the Count’s favorite number: 34,969.

Conclusion

So, how many colors are there? I dunno. It depends on how you ask the question and who you ask. Pick a number between 3 and 16,777,216.

[1] SEM images are still back in the days of black and white. If you see an SEM image with any other colors in it, it has been colorized. Someday, someone will figger out how to make electrons with different colors, and then the images will be really, really cool. I think I’ll go file for a patent on that idea.

[2] The chromaticity diagram was an early attempt at trying to turn the spectral response of the eye into something that explained our perception of color. It was replaced by other mathematical models (in particular, CIELAB), but is still the easiest way to understand the gamut of a set of light sources.

[3] Sharp introduced the Aquos Quattron display in September of 2010 which added a fourth color of pixel, yellow. For this monitor, the gamut is expanded into a quadrilateral that gives you more yellow and orange colors.

[4] Speaking of orange… I think that carrots are a richer orange than oranges are. I think we should swap the names of these too foods.

[5] Ok, I was just kidding about that one. Reddish green isn’t a color; it’s the name of the band I am going to form after I retire from all this color stuff and learn to play the sax.

[6] CIELAB was the next big step forward in coming up with a measurable number that corresponds intuitively to our perception of color. For dinner, a movie, and plane tickets, I will come to your living room and give the CIELAB lecture to you and ten of your most intimate friends.